Fibonacci’s

Infinity

FINE ART

The golden ratio is an irrational number approximately equal to 1.618. It exists when a line is divided into two parts, with one part longer than the other. The longer part (a) divided by the smaller part (b) is equal to the sum of (a) + (b) divided by (a), which both equal ~1.618.

Theorem 1
In a golden rectangle, if you remove the square built on the short side, you still get a golden rectangle.

Demonstration :
The length of the remaining rectangle is l and its width is L – l, and:

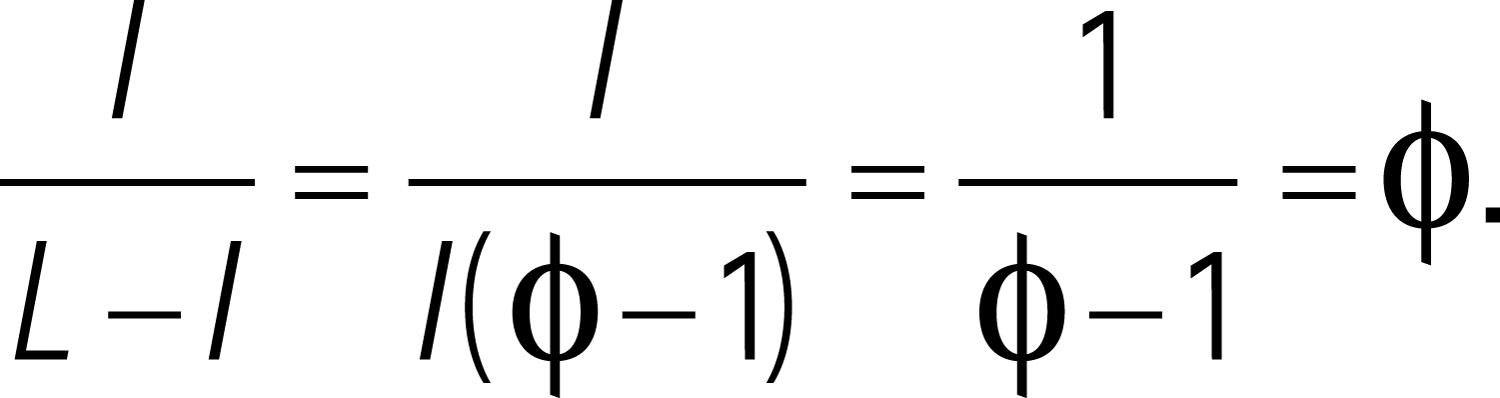
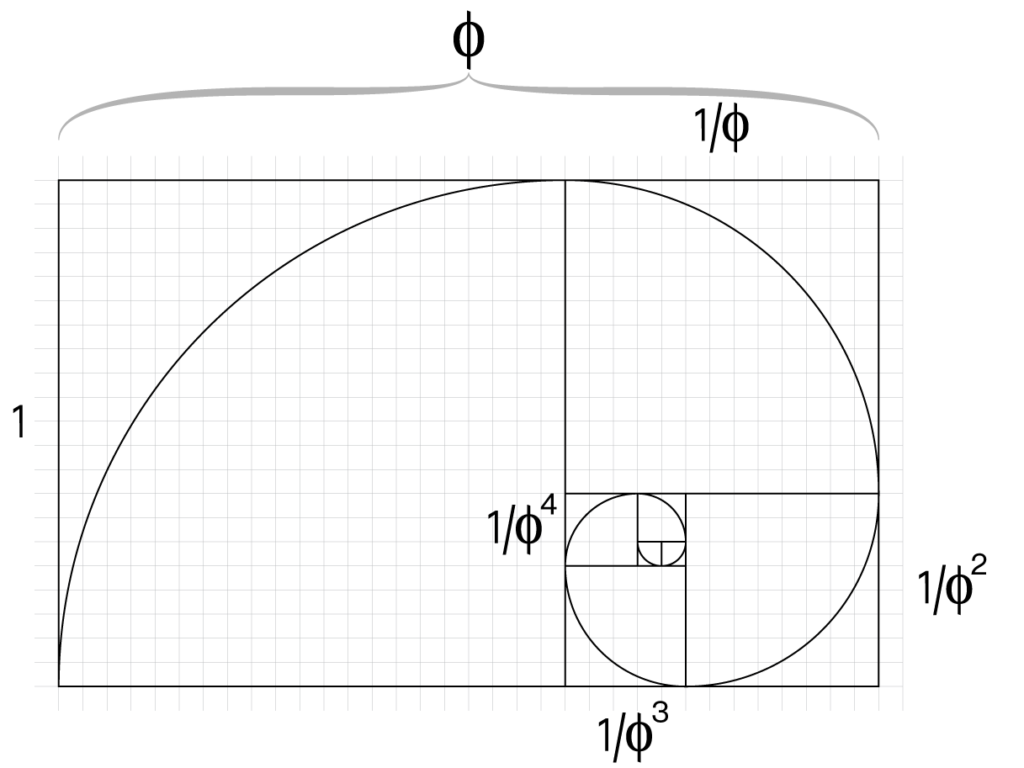
Way back in my Junior High days, I remember a sequence of numbers taught in class: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc. Obtained by adding 1+1=2; 1+2=3; 2+3=5; 3+5=8; 5+8=13; 8+13=21, and so on. Like most school dropouts, I wasn’t really listening and hadn’t retained the fact that this sequence of numbers was in relation to the golden ratio. Only later did I realize how all of this was marvellous inspiration to create.

Inspired by all of this mathematical brilliance, so began my visualizations of Fibonacci’s theorem which evolved into this series of paintings titled Fibonacci’s Infinity, a mathematical equation brought to life in all of its visual splendour.

All images © 2023 Rodolphe Charpentier. All Rights Reserved